Matematik bazılarımız için zor, bazılarımız için ise eğlenceli bir uğraş olarak görülmektedir. Geçmişte, kendi hayatlarını matematik bilimi üzerine adayan ünlü matematikçiler bizlere zorluğun göreceli bir kavram olduğunu çok iyi bir şekilde anlatmışlardır. Matematik evrenin her yerinde olduğu gibi yaşamımız boyunca, günlük işlerimizde dahi onunla yaşadığımız bir kavramdır. Bu yazımızda sizler için hayatımızın her yerinde olan matematiği bizlere anlatan ve bu bilime katkısı olan ünlü matematikçiler ‘den bahsedeceğiz.
En Ünlü Matematikçiler
PISAGOR

”Evrenin hakimi sayıdır. Sayılar evreni yönetiyor.” sözünün sahibi Somos’lu Pisagor’un İsa’dan önce 596 yıllarında doğduğu tahmin edilmektedir. Yunan asıllı olan ünlü matematikçi ve filozof ülkesinde hüküm süren politik baskılardan kaçarak İtalya’nın güneyinde Kroton şehrine gelmiş ve okulunu burada açarak şöhrete kavuşmuştur. ”Geometride, aksiyomlar ve postülatlar her şeyden önce gelmelidir. Sonuçlar bu aksiyom ve postülatlardan yararlanılarak elde edilmelidir” düşüncesini ilk bulan ve ilk uygulayan matematikçi Pisagor’dur. Matematiğe aksiyomatik düşünceyi ve ispat fikrini getiren yine Pisagor’dur. Çarpma cetvelinin bulunuşu ve geometriye uygulanması da Pisagor tarafından yapılmıştır.
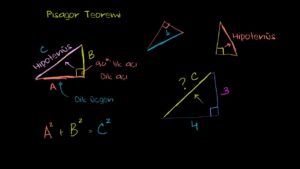
Pisagor’un adını 2.600 yıldır yaşatan ve onun ün kazanmasını sağlayan teoremi ise: Bir dik üçgende, dik kenarlar üzerine kurulan karelerin alanlarının toplamı, hipotenüs üzerine kurulan karenin alanına eşittir. Pisagor teoremi, rasyonel sayılarla ölçülemeyen uzunluğun da var olduğunu gösterir. Pisagor’un matematik, fizik, astronomi, felsefe ve müzikte getirmek istediği yenilik, buluşlar ve ışıkları hazmedemeyen bir takım siyaset ve din yobazları halkı Pisagor’a karşı ayaklandırarak okulunu ateşe vermişler, Pisagor ve öğrencileri bu okulun içinde alevler arasında İ.Ö.500 yıllarında ölmüşlerdir. Pisagor’un ve öğrencilerinin çalışmalarının birçoğu bu alevler arasında yok olup gitmiştir.
ÖKLID

Yunanlı bir matematikçi olan Öklid, M.Ö. 330 – 275 yılları arasında yaşamıştır. İskenderiyeli olan Öklid, geometrideki yerini kendi zamanına kadar bilinen kavramları ”Öğeler” ismini verdiği kitabında toplamıştır. Aslında Öğeler bir derlemedir ve 13 ciltten oluşmaktadır. Öklid, Öğeler isimli kitabında kanıta ihtiyaç duymayan 5 aksiyom ortaya koymuştur. Diğer önermelerin tamamını ise bu aksiyomlarla çıkarmıştır. Bu 5 aksiyom ise şöyledir;
- İki noktadan yalnız bir doğru geçer.
- Bir doğru parçası iki yöne de sınırsız bir şekilde uzatılabilir.
- Merkezi ve üzerinde bir noktası verilen bir çember çizilebilir.
- Bir doğruya dışında alınan bir noktadan bir ve yalnız bir paralel çizilebilir.
- Bütün dik açılar birbirine eşittir.
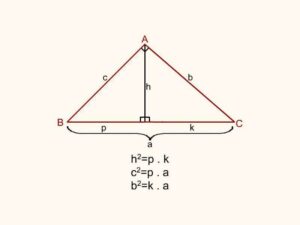
Öklid bağıntısı ise; bir dik üçgende, dik açının olduğu köşeden hipotenüse yani karşı kenara dikme indirilirse, resimde de gördüğünüz gibi eşitlikler oluşur ve bu eşitliklere Öklid teoremi yada Öklid bağıntıları denir.
F. BERNHARD RIEMANN

Bernhard Riemann, 1826’da fakir bir ailede doğmasından 19. yüzyılın en seçkin matematikçilerinden birisi olmasına kadar uzanan hayatıyla ilgi çeker. Geometriye olan katkıları son derece geniş olmakla beraber matematikte kendi ismiyle anılan teoremlerin sayısı da bir hayli fazladır: Riemann Geometrisi, Riemann Yüzeyleri ve Riemann İntegrali gibi. İsminin en çok telaffuz edildiği ve efsanevi derecede zor olmasıyla da nam salmış Riemann Hipotezi ise asal sayıların dağılımıyla ilgili oldukça karışık bir problemdir. Çok az sayıda matematikçinin anlayabilmesi yüzünden, ortaya çıkışından sonraki 50 sene kadar fark edilemeyen bu problem, değerinin anlaşılmasıyla birlikte bilimsel arenada bir anda sonucu en çok merak edilenler listesine girmiştir ve en muhteşem matematikçileri bile ne yapacaklarını bilemez duruma düşürmüştür.
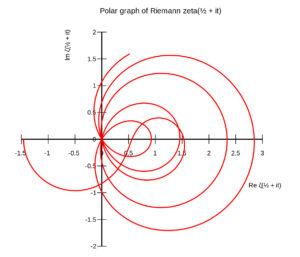
1854’te bir fonksiyonun trigonometrik serilerle gösterilmesini konu alan doçentlik tezinde, türevlenmeyen sürekli bir fonksiyon örneği verdi. Aynı incelemesinde Cauchy’nin kuramından daha genel bir integralleme kuramı geliştirdi. Bu kuram, süreksizlik bakımından sayısız bir sonsuzluğu olan sınırlı fonksiyonlara uygulanabiliyordu. Oysa Cauchy’nin kuramı, yalnızca parça parça sürekli fonksiyonlar için geçerliydi. Sayılar kuramında zeka fonksiyonunun, asal sayıların aritmetik kuramı için önemini gösterdi. Riemann eğriliği pozitif olan katlı uzaylar üzerinde, koşulsuz Öklidçi olmayan bir geometri geliştirdi.
GEORGE BOOLE

Nam- ı diğer bilgisayar biliminin babası olan George Boole 2 Kasım 1815’te İngiltere’nin Lincoln kasabasında dünyaya gelmiştir. Matematik ve mantık bilimlerinin yanı sıra felsefe, ilahiyat ve edebiyatla da ilgilenmiştir. 1841’de Boole Analitik Dönüşümler Teorisi Üzerine Araştırmalar isimli ilk çalışması, Cambridge Matematik Dergisi’nde yayımlanmıştır. Genel Metot Analizi üzerine en ünlü makalelerinden biriside Royal Society’s Philosophical Transactions da yer almıştır.
1844 yılında Philosophical Transactions of the Royal Society adlı dergide yayınlanan önemli bir makalesinde, cebir ile diferansiyel ve integral hesap yöntemlerinin nasıl birleştirilebileceğini irdelemiştir. Aynı yıl analize, yani cebir ile diferansiyel ve integral hesap yöntemlerinin sonsuz büyük ve sonsuz küçük nicelikler için kullanılmasına ilişkin katkılarından ötürü Royal Society’nin bir madalyasıyla ödüllendirilen Boole, çok geçmeden kendi cebrinin mantıkta da uygulanabileceği kanısına varmıştır. Mantığın felsefe yerine matematikle birlikte ele alınması gerektiğini savunan George Boole, 1854 yılında da Mantık ve Olasılıklara İlişkin Matematiksel Kuramların Dayandığı Düşünce Yasaları üzerine bir incelemeyi kaleme almıştır. Bu çalışmasında Boole, sınıfların cebrini tanıtmıştır. George Boole hakkında detaylı bilgi edinmek isterseniz ”George Boole kimdir?” adlı makalemizi inceleyebilirsiniz.
HAREZMİ

Tam adı Muhammed Bin Musa el-Harezmi olan bu büyük bilim adamı, Horasan’da doğmuştur. Bugünkü cebir ve trigonometrinin kurucusudur. Avrupa’nın en çok yararlandığı matematikçidir. Cebir üzerine çok sayıda eser vermiştir. Descartes’e kadar batı bilim dünyasında egemen olan Harezmi ve Harezmi cebriydi. Bu nedenle Harezmi dünya çapında ünlü matematikçilerden biridir. En önemli eseri, Cebir ve Mukayese Hesabı’dır. Deneyler, enlem ve boylam kitapları ve bir de gökyüzü atlası vardır. Hindistan matematiğini dünyaya tanıtan yine Harezmi’dir.
RENE DESCARTES

Fransız matematikçi, filozof ve fizikçi Rene Descartes ”Düşünüyorum o halde varım.” felsefesiyle bilinmektedir. 1596 ile 1650 yılları arasında yaşayan bu Fransız, matematikte de büyük etkiler bırakmıştır. Descartes modern Kalkülüs’ün temellerini ortaya çıkarmasıyla günümüze kadar gelen süreci başlatmıştır. Ancak Descartes özel olarak Kartezyen Geometriyi (kareli düzlemde x ve y eksenleriyle konum belirlemeyi) geliştiren ve cebiri de bu yöntemle birleştirerek yeni bir çığır açan matematikçi olarak tarihteki yerini almıştır. Bu gelişmeden önce çoğu geometrici sanatlarını icra etmek için sade, çizgisiz kâğıtlar veya yüzeyler kullanıyordu. Bu yüzden de yapılan işler üzerinde uzaklıklar elle ölçülüyordu. Kartezyen geometri ile bu durum büyük bir hızla değişti ve noktaların yeri artık grafik üzerinde belirtilebildiğinden çeşitli ölçeklere uyarlanabilen grafik çizimlerine başlandı.
Matematiğe yaptığı en son katkılardan bir tanesi de “Descartes İşaret Kuralı” olarak adlandırılan ve polinom denklemlerin köklerini bulmak için kullanılan yöntemi geliştirmesidir. Descartes, “İlk Felsefe Üzerine Meditasyonlar” isimli eseriyle bugünkü üniversitelerin felsefe bölümlerinde okutulmasının yanında modern matematiksel ifadelere olan katkılarıyla da matematik dünyasının büyük öncülerinden bir tanesidir.
ÖMER HAYYAM

Asıl adı Gıyasettin Ebu’l Feth Bin İbrahim El Hayyam’dır. 18 Mayıs 1048’de İran’ın Nişabur kentinde doğmuştur. Tıp, fizik, astronomi, cebir, geometri ve yüksek matematik alanlarında önemli çalışmaları olan Ömer Hayyam için zamanın bütün bilgilerini bildiği söylenirdi. O herkesten farklı olarak yaptığı çalışmaların çoğunu kaleme almadı, oysa O ismini çokça duyduğumuz teoremlerin isimsiz kahramanıdır. En büyük eseri Cebir Risalesi’dir. On bölümden oluşan bu kitabın dört bölümünde kübik denklemleri incelemiş ve bu denklemleri sınıflandırmıştır. Matematik tarihinde ilk kez bu sınıflandırmayı yapan kişidir. O cebri, sayısal ve geometrik bilinmeyenlerin belirlenmesini amaçlayan bilim olarak tanımlardı. Matematik bilgisi ve yeteneği zamanın çok ötesinde olan Ömer Hayyam denklemlerle ilgili başarılı çalışmalar yapmıştır. Nitekim, Hayyam 13 farklı 3. dereceden denklem tanımlamıştır. Denklemleri çoğunlukla geometrik metod kullanarak çözmüştür ve bu çözümler zekice seçilmiş konikler üzerine dayandırılmıştır. Bunun yanı sıra Hayyam, binom açılımını da bulmuştur. Binom teoremini ve bu açılımdaki katsayıları bulan ilk kişi olduğu düşünülmektedir.


